1) Área do retângulo:

Por definição o retângulo é um quadrilátero equiângulo (todos os seus ângulos internos são iguais), cujos lados opostos são iguais.

Se todos os seus quatro lados forem iguais, teremos um tipo especial de retângulo, chamado de quadrado.

Por ser o retângulo um paralelogramo, o cálculo da sua área é realizado da mesma forma.

Se denominarmos as medidas dos lados de um retângulo como na figura ao lado, teremos a seguinte fórmula:

2) Área do quadrado:

Todo quadrado é também um losango, mas nem todo losango vem a ser um quadrado, do mesmo modo que todo quadrado é um retângulo, mas nem todo retângulo é um quadrado.

O quadrado é um losango, que além de possuir quatro lados iguais, com diagonais perpendiculares, ainda possui todos os seus ângulos internos iguais a 90°.

Observe ainda que além de perpendiculares, as diagonais também são iguais.

Por ser o quadrado um losango e por ser o losango um paralelogramo, podemos utilizar para o cálculo da área do quadrado, as mesmas fórmulas utilizadas para o cálculo da área tanto do losango, quanto do paralelogramo.

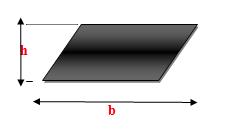
3) Área do paralelogramo:

Um quadrilátero cujos lados opostos são iguais e paralelos é denominado paralelogramo.

Com h representando a medida da sua altura e com b representando a medida da sua base, a área do paralelogramo pode ser obtida multiplicando-se b por h, tal como na fórmula abaixo:

4) Área do losango:

O losango é um tipo particular de paralelogramo. Neste caso além dos lados opostos serem paralelos, todos os quatro lados são iguais.

Se você dispuser do valor das medidas h e b, você poderá utilizar a fórmula do paralelogramo para obter a área do losango.

Outra característica do losango é que as suas diagonais são perpendiculares.

Consideremos a base b como a metade da diagonal d₁ e a altura h como a metade da diagonal d₂, para calcularmos a área de um destes quatro triângulos. Bastará então que a multipliquemos por 4, para obtermos a área do losango. Vejamos:

5) Área do trapézio:

O trapézio é um quadrilátero que possui dois lados paralelos chamados de base maior e base menor e dois lados não paralelos.

Considere um trapézio de base maior B, base menor b e altura h.

6) Área do triângulo:

Denominamos de triângulo a um polígono de três lados.

A letra h representa a medida da altura do triângulo, assim como letra b representa a medida da sua base.

A área do triângulo será metade do produto do valor da medida da base, pelo valor da medida da altura, tal como na fórmula abaixo:

7) Área de um triângulo equilátero:

O triângulo é considerado o polígono mais simples da geometria plana e o mais importante, levando em consideração as características de seu formato. Estruturas de sustentação são construídas no formato triangular, em razão da segurança obtida.

Existem três modelos de triângulos quanto à medida dos seus lados:

Escaleno: os lados possuem medidas diferentes.
Isósceles: possui dois de seus lados com medidas iguais.
Equilátero: possui todos os lados com mesma medida.

8) Área de polígonos regulares:

Todo polígono regular pode ser inscrito em uma circunferência. Ao decompormos esse polígono notamos várias regiões triangulares, então se o polígono for decomposto em n triângulos basta calcularmos sua área e multiplicarmos pelo número de triângulos.

O número de lados da figura é igual ao número de triângulos que compõem a figura.

No pentágono inscrito abaixo podemos notar que a altura de cada triângulo que o compõe corresponde ao apótema do polígono, podemos substituir a altura h pelo apótema a, na expressão que calcula a área de cada triângulo:

9) Área da superfície de um cilindro reto:

a) Área de um círculo:

A área do círculo é diretamente proporcional ao raio, que é a distância entre o centro e a sua extremidade. Para calcularmos a área do círculo, utilizamos a expressão matemática que relaciona o raio e a letra grega π (pi), que corresponde a, aproximadamente, 3,14.

O círculo é determinado de acordo com o aumento do número de lados de um polígono.

b) Área do setor circular:

O setor de um círculo é uma região delimitada por dois segmentos de retas que partem do centro para a circunferência. Esses segmentos de reta são os raios do círculo.

O ângulo α é chamado de ângulo central.

Dessa forma, percebemos que o setor circular é uma parte da região circular, ou seja, ele é uma fração da área do círculo.

Assim podemos afirmar que a área do setor circular é diretamente proporcional ao valor de α, pois a área de todo o círculo é diretamente proporcional a 360º.

Assim podemos montar a seguinte relação (regra de três):

10) Área da superfície do cilindro reto:

A superfície de um cilindro reto de altura h e raio da base r é equivalente à reunião de uma região retangular, de lados 2πr e h, com dois círculos de raio r. Observe a planificação do cilindro.