Poliedros

• Toda figura Geométrica, de três dimensões, formada por polígonos é chamada de Poliedro. Os poliedros possuem faces, arestas e vértices.

• Faces: É a superfície de um poliedro formada por polígonos.

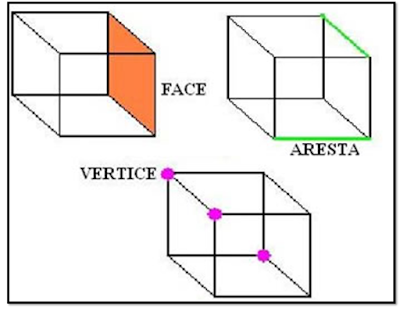
• Arestas: São os lados de cada face de um poliedro.












• Vértices: É formada pelo encontro de duas retas (arestas).

• Os poliedros são classificados de acordo o número de faces.

• Relação de Euler:

Some os números de vértices e faces e compare-os com o número de arestas. Você verá que a soma será duas unidades maior que o número de arestas. Se generalizarmos

essa ideia, teremos:     V + F = A + 2  

Essa equação representa a Relação de Euler.

"Em todo poliedro convexo V - A + F - 2 ",

onde: V= número de vértices

A= número de arestas

F= número de faces

• Teorema de plantão:

"Existem 5 e somente 5 poliedros regulares."

Demonstração:
Consideremos um poliedro com F (faces), V (vértices) e A (arestas), onde cada face tem n lados e cada vértice tem p arestas.

Sabemos que: 

Sabemos ainda que:
n e p são maiores ou iguais a 3
Fazendo tentativas atribuindo valores crescente a, n e p teremos como poliedros regulares apenas os Tetraedro, Hexaedro (cubo), Octaedro, Dodecaedro, Icosaedro.

• Poliedros de plantão:

FONTES:

http://www.alunosonline.com.br/matematica/relacao-euler.html
http://objetoseducacionais2.mec.gov.br/bitstream/handle/mec/10483/open/file/geo1001.htm
http://educacao.uol.com.br/matematica/poliedro.jhtm

ALUNOS: Bruna Pereira, Eleonara Santos, Jonatas Cruz e Josinete Alves. (3º B vespertino)