Apresentação do Seminário (Esfera)

Componente: Alef Souza

Esfera

• Chamamos de esfera de centro O e raio R o conjunto de pontos do espaço cuja distância do centro é menor ou igual a ao raio R. Considerando a rotação completa de um semicírculo em torno de um eixo e, a esfera é o sólido gerado por essa rotação. Assim, ela é limitada por uma superfície esférica e formada por todos os pontos pertencentes a essa superfície e ao seu interior: 

        

• O volume da esfera de raio R é dado por:

• A área da superfície esférica, é dada por:

• Zona esférica é a parte da esfera gerada do seguinte modo:

A área da zona esférica é dada por: 2. pi. R. h

• Calota esférica é a parte da esfera gerada do seguinte modo:

A área da calota esférica é dada por: 2. pi. R. h

• O fuso esférico é uma parte da superfície esférica que se obtém ao girar uma semi-circunferência de um ângulo  em torno do seu eixo:

A área do fuso esférico pode ser obtida por uma regra de três:

• A cunha esférica é a parte da esfera que se obtém ao girar um semicírculo em torno do seu eixo de um ângulo :

O volume da cunha pode ser obtido por uma regra de três:

Aluno: Alef Souza  (3º B, VESPERTINO)

Apresentação do Seminário (Grupo de Cone)

Componentes: Adriele Aragão, Evelyn Melo, Josias Aragão e Willanna Santana

Roda de Conversa (Cone)

• O grupo fez uma roda na sala, e optou por um jogo de verdeiro/falso e desafio. Colocavam a caneta pra rodar, e na pessoa que parava,  tinha que responder uma pergunta. A medida que as pessoas iam respondendo, o grupo esclarecia as perguntas propostas.

CONE

ALUNOS: Adriele Aragão, Evelyn Melo, Josias Aragão e Willanna Santana (3º B, VESPERTINO)

Apresentação do Seminário (Grupo de Cilindro)

                                   Componentes: Aline Silva, Ramon Leal e Ursula de Jesus

Roda de Conversa (Cilindro)

• O grupo fez um jogo de forca, envolvendo algumas perguntas sobre o assunto, ganhou o grupo que acertou mais questões. 

Cilindro

•  Bases são os círculos paralelos de raio r e centros O e O';
•  As geratrizes são os segmentos paralelos a OO'  com extremidades nas circunferências das bases, podendo ser classificada como oblíquas as bases chamamos de cilindro oblíquo, e quando são perpendiculares às bases, cilindro reto;
•   O eixo é a reta OO';
• Altura h é a distância entre os planos das bases;
•   Superfície lateral é a reunião de todas as geratrizes;
•  Em um cilindro oblíquo, a seção meridiana é um paralelogramo;
•  Em um cilindro reto, a seção meridiana é um triângulo.

•  Área da base: Ab = (pi)r²
•   Área lateral:   Al = 2(pi)rh
•   Área total da superfície: At = 2Ab + Al = 2(pi)r² + 2(pi)rh = At = 2(pi)r (r + h)
•   Medida da circunferência: C= 2(pi)r
•   Altura total: At = 2Ab + Ac
• O número de (pi) sempre será  3, 14
•  Pelo Princípio de Cavalieri o  volume do cilindro será, V = Ab · h ou V = (pi)r²  h
•  CILINDRO DE REVOLUÇÃO: O cilindro reto também pode ser classificado cilindro de revolução, podendo ser gerado pela rotação de uma região retangular em torno de um eixo.

ALUNOS: Aline Silva, Ramon Leal e Ursula de Jesus. (3º B, VESPERTINO)

Apresentação do Seminário (Grupo de Pirâmide)

Componentes: Jassilene, Mayane, Taciane e Tamiles

Videos da apresentação (PRISMAS)

OBS: Lembrando que, os vídeos não contém toda apresentação. 

 

                                                                       

Roda de Conversa (Pirâmide)

•  O grupo optou por um jogo, no qual faziam perguntas aos outros grupos, até que um saísse ganhador. Ajudando assim as pessoas compreenderem o assunto de uma forma dinâmica.

Apresentação do Seminário (Grupo de Prismas)

Componentes: Elves Ramos, Joanna D'arc, Layla Fortunato e Mateus Queiroz

Prismas

FONTES:
http://www.estudopratico.com.br/prismas/
http://www.somatematica.com.br/emedio/espacial/espacial11.php
http://www.somatematica.com.br/emedio/espacial/espacial12.php


ALUNOS: Elves Ramos, Joanna D'arc, Layla Fortunato e Mateus Queiroz (3º B, VESPERTINO)

Roda de Conversa (Prismas)

• Os componentes do grupo PRISMA, optaram por uma dinâmica. Na qual os outros grupos se reuniram, para responderem as questões que estavam sendo perguntadas. 

Apresentação do Seminário (Grupo de Área e Poliedros)

Grupo 02: POLIEDROS 

Componentes: Bruna Pereira, Eleonara Santos, Jonatas Cruz e Josinete Alves

Grupo 01: ÁREA 

Componentes: Bruno Ribeiro, Elielton Gomes, Joyce Brandão e Vanuza Bastos

Poliedros

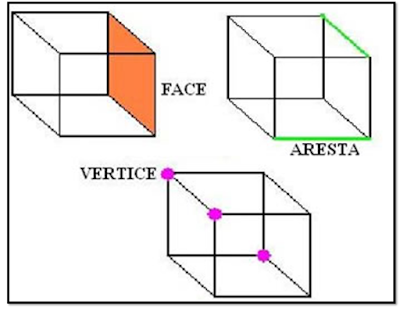
• Toda figura Geométrica, de três dimensões, formada por polígonos é chamada de Poliedro. Os poliedros possuem faces, arestas e vértices.

• Faces: É a superfície de um poliedro formada por polígonos.

• Arestas: São os lados de cada face de um poliedro.












• Vértices: É formada pelo encontro de duas retas (arestas).

• Os poliedros são classificados de acordo o número de faces.

• Relação de Euler:

Some os números de vértices e faces e compare-os com o número de arestas. Você verá que a soma será duas unidades maior que o número de arestas. Se generalizarmos

essa ideia, teremos:     V + F = A + 2  

Essa equação representa a Relação de Euler.

"Em todo poliedro convexo V - A + F - 2 ",

onde: V= número de vértices

A= número de arestas

F= número de faces

• Teorema de plantão:

"Existem 5 e somente 5 poliedros regulares."

Demonstração:
Consideremos um poliedro com F (faces), V (vértices) e A (arestas), onde cada face tem n lados e cada vértice tem p arestas.

Sabemos que: 

Sabemos ainda que:
n e p são maiores ou iguais a 3
Fazendo tentativas atribuindo valores crescente a, n e p teremos como poliedros regulares apenas os Tetraedro, Hexaedro (cubo), Octaedro, Dodecaedro, Icosaedro.

• Poliedros de plantão:

FONTES:

http://www.alunosonline.com.br/matematica/relacao-euler.html
http://objetoseducacionais2.mec.gov.br/bitstream/handle/mec/10483/open/file/geo1001.htm
http://educacao.uol.com.br/matematica/poliedro.jhtm

ALUNOS: Bruna Pereira, Eleonara Santos, Jonatas Cruz e Josinete Alves. (3º B vespertino)